https://www.acmicpc.net/problem/2565
2565번: 전깃줄
첫째 줄에는 두 전봇대 사이의 전깃줄의 개수가 주어진다. 전깃줄의 개수는 100 이하의 자연수이다. 둘째 줄부터 한 줄에 하나씩 전깃줄이 A전봇대와 연결되는 위치의 번호와 B전봇대와 연결되는
www.acmicpc.net
문제
두 전봇대 A와 B 사이에 하나 둘씩 전깃줄을 추가하다 보니 전깃줄이 서로 교차하는 경우가 발생하였다. 합선의 위험이 있어 이들 중 몇 개의 전깃줄을 없애 전깃줄이 교차하지 않도록 만들려고 한다.
예를 들어, < 그림 1 >과 같이 전깃줄이 연결되어 있는 경우 A의 1번 위치와 B의 8번 위치를 잇는 전깃줄, A의 3번 위치와 B의 9번 위치를 잇는 전깃줄, A의 4번 위치와 B의 1번 위치를 잇는 전깃줄을 없애면 남아있는 모든 전깃줄이 서로 교차하지 않게 된다.
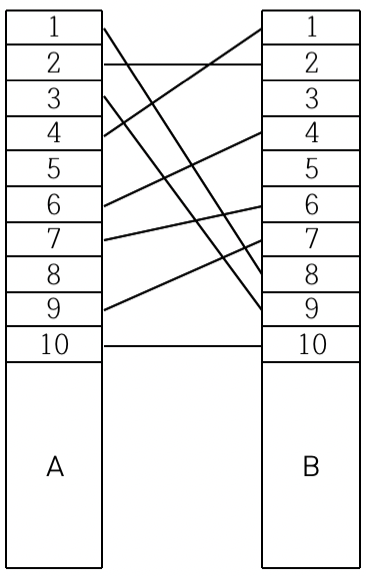
전깃줄이 전봇대에 연결되는 위치는 전봇대 위에서부터 차례대로 번호가 매겨진다. 전깃줄의 개수와 전깃줄들이 두 전봇대에 연결되는 위치의 번호가 주어질 때, 남아있는 모든 전깃줄이 서로 교차하지 않게 하기 위해 없애야 하는 전깃줄의 최소 개수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에는 두 전봇대 사이의 전깃줄의 개수가 주어진다. 전깃줄의 개수는 100 이하의 자연수이다. 둘째 줄부터 한 줄에 하나씩 전깃줄이 A전봇대와 연결되는 위치의 번호와 B전봇대와 연결되는 위치의 번호가 차례로 주어진다. 위치의 번호는 500 이하의 자연수이고, 같은 위치에 두 개 이상의 전깃줄이 연결될 수 없다.
출력
첫째 줄에 남아있는 모든 전깃줄이 서로 교차하지 않게 하기 위해 없애야 하는 전깃줄의 최소 개수를 출력한다.
위 문제는 DP를 이용해서 풀이하는 문제인데 재귀를 활용하여 풀다보니 많은 시간 소모가 된다고 판단했고 다흔 방식에 대해 고민하다 해결책이 떠오르지 않아 다른 블로그를 참고 했다.
(참고: https://zidarn87.tistory.com/291)
참고한 블로그처럼 0-index 혹은 1-index를 기준으로 정렬을 해서 문제를 풀이하는 것은 이해를 했지만, 그 다음 풀이법에 대해 어려움이 있었는데 증가하는 사다리의 각 위치까지 증가하는 사다리 수의 최댓값을 을구해서 이를 전체 길이에서 빼주면 된다는 것을 알게 되었다.
위 문제에서 처럼 정렬을 했을 때,
1 8
2 2
3 9
4 1
6 4
7 6
9 7
10 10
사다리가 이렇게 놓여진다.
왼쪽을 기준으로 정렬을 했으므로 우리는 오르쪽 사다리의 위치만 보면 된다.
위에서부터 위치를 보았을 때, 1 > 4 > 6 > 7 > 10 의 사다리 갯수가 가장 긴 방식이므로 나머지 2개를 지워주면 된다.
이런식으로 코드를 구성하면,
import sys
input = sys.stdin.readline
n = int(input())
# 사다리가 연결된 값을 입력받고 0-index or 1-index를 기준으로 정렬을 해준다.
ladders = [list(map(int, input().split())) for _ in range(n)]
ladders.sort()
# 각 위치의 사다리의 갯수를 1로 초기화 해준다.
dp = [1 for _ in range(n)]
# 최대 길이를 업데이트할 변수
l = 0
for i in range(n):
for j in range(i):
# 0 ~ i 까지 다시 비교하여 연속으로 증가하는 사다리의 갯수를 j-index에 업데이트 해줍니다.
if ladders[i][1] > ladders[j][1]:
dp[i] = max(dp[i], dp[j] + 1)
# 사다리 갯수의 최댓값을 l에 업데이트
l = max(l, dp[i])
# 위에서 구한 최댓값은 전체 길이 n에서 빼준 값을 출력
print(n - l)
해당 게시글이 도움이 되었다면,
'IT 톺아보기 > 알고리즘' 카테고리의 다른 글
| 백준 2470번 두 용액 | python (1) | 2023.01.25 |
|---|---|
| 백준 1966번 프린터 큐 | python (0) | 2023.01.24 |
| 백준 1644번 | 소수의 연속합 - python (0) | 2022.11.20 |
| 백준 1197번 | 최소 스패닝 트리 - python (0) | 2022.11.20 |
| 백준 1647번 | 도시 분할 계획 - python (0) | 2022.11.20 |


